피타고라스 정리는 수학의 기초적인 정리 중 하나로, 직각삼각형에서 두 변의 길이와 빗변의 길이 사이의 관계를 보여주는 공식입니다. 고등학교때 다들 배우죠.
사실 이 정리는 다양한 분야와 일상생활에서도 매우 유용하게 활용되는데요, 오늘은 피타고라스의 정리가 일상생활에 미치는 영향에 대해 살펴보겠습니다.
피타고라스 정리 활용 분야
피타고라스의 정리(Pythagorean theorem)가 사용되는 분야가 어디가 있을까요 ?
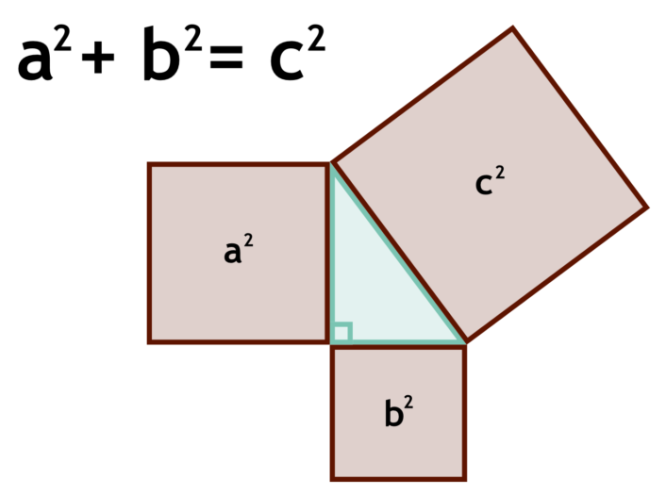
피타고라스 정리는 직각삼각형의 두 직각변의 제곱의 합이 빗변의 제곱과 같다는 겁니다.
얼핏 단순해 보이는 이 정리는 두 지점간의 거리와 높이를 측정해야 하는 모든 상황에서 위력을 발휘합니다.
건축 설계에서 교량의 기둥간 거리와 기둥의 높이를 측정 해야 한다거나, 측량사들이 두 점사이의 거리를 계산해야 할 때 사용 되죠.
컴퓨터 그래픽에서도 화면상의 점들 사이를 계산 할 때 피타고라스 정리는 필수적입니다.
우리가 늘상 사용하고 있는 GPS와 카 네비게이션이 위치와 경로를 구하는 방식에서도 피타고라스 정리가 사용된다고 보시면 됩니다.
이 뿐만 아니라, 농구나 축구 같은 스포츠의 비디오 분석 시간에 선수들 사이의 거리를 계산하고 전략을 세울 때에도 피타고라스 정리는 필요하죠.
이렇듯 학교에서 수학시간에만 쓰는 줄 알고 배웠던 피타고라스 정리가 실제 생활에서도 많이 사용되고 있습니다.
피타고라스 생애와 업적
고대 그리스의 위대한 수학자이자 철학자인 피타고라스는 기원전 570년경 그리스의 사모스 섬에서 태어났습니다. 그는 청년 시절에 여러 나라를 여행하며 다양한 문화를 접하고 지식을 쌓았습니다.
피타고라스는 특히 이집트에서 많은 시간을 보내며 수학과 천문학, 그리고 종교적인 신비주의에 대한 깊은 관심을 갖게 된 것으로 알려져 있습니다.
그가 이룬 업적중 가장 유명한 것은 역시 피타고라스의 정리이죠.
피타고라스 학파
피타고라스는 기원전 530년경 남부 이탈리아의 크로톤에 피타고라스 학파를 설립했습니다. 이 학파는 철학적이고 종교적인 공동체로, 수학적 연구와 더불어 영혼의 순수성을 강조하는 신비주의적인 교리를 따랐습니다.
피타고라스 학파는 수를 신성한 것으로 여기며, “모든 것은 수이다”라는 철학적 입장을 취했습니다.
피타고라스의 금지령
피타고라스 학파는 여러 가지 엄격한 규율을 가지고 있었습니다. 그 중 하나는 특정 음식을 먹지 않는 것이었는데, 특히 콩을 먹는 것을 금지했습니다.
이 금지령의 이유는 명확하지 않지만, 콩이 영혼의 순수성을 해친다고 믿었거나, 콩의 속이 사람의 내장을 닮았다고 여겼기 때문일 수 있습니다.
피타고라스와 황금비
피타고라스 학파는 황금비를 발견하고 그 비율을 다양한 예술과 건축에 적용했습니다. 황금비는 두 길이의 비율로, 그 비율이 대략 1:1.618에 해당합니다.
이는 아름다움과 조화의 비율로 여겨져, 피타고라스 학파는 이를 신성한 비율로 간주했습니다.
죽음과 유산
피타고라스의 죽음에 대해서는 여러 설이 있습니다. 어떤 전설에 따르면, 그가 적대적인 정치적 세력에 의해 추방되어 결국 사망했다고도 합니다.
또 다른 이야기로는, 그가 도망치던 중 콩밭을 가로지르는 것을 거부하다가 붙잡혀 죽었다고도 합니다. 피타고라스의 유산은 그의 수학적 업적뿐만 아니라 철학과 종교에 대한 영향력에도 반영되어 있습니다.
무리수의 발견
피타고라스와 그의 학파는 수학의 기초를 닦은 것으로 잘 알려져 있지만, 그들의 연구가 이끈 무리수(irrational numbers)의 발견은 피타고라스와 그의 제자들에게 큰 충격을 주었습니다.
무리수의 개념은 당시의 철학적, 수학적 신념을 뒤흔들었고, 이에 대한 피타고라스 학파의 반응은 꽤 흥미로웠는데요. 당시에는 수학에 <무리수>는 없고 <유리수>만 있었습니다. <유리수>는 흔히 분수 형태로 표현이 가능한 수로 분모가 0이 아닌 수를 말하는데요. 쉽게 말하면 그냥 분수 입니다.
한편 피타고라스의 정리에 따르면, 우리는 직각 삼각형의 빗변의 길이를 구할 수 있는데요. 문제는 유리수로 표현이 안되는 경우가 발생하더라는 거죠.
예를 들어, 밑변과 높이가 각각 1인 직각 삼각형이라면 빗변의 길이는 제곱하면 2가 나오는 수 – 즉 루트 2- 가 나오는 데, 이 당시까지 이러한 무리수는 발견되지 않았었거든요.
히파수스의 이야기
피타고라스학파의 구성원 중 히파수스(Hippasus)가 무리수를 처음으로 발견했다고 전해집니다. 그는 빗변이 1인 직각삼각형의 빗변 길이인 루트2가 유리수가 아니라는 것을 증명했습니다.
이는 피타고라스학파의 “모든 수는 유리수”라는 믿음을 깨뜨리는 발견이었습니다.
전설에 따르면, 당시 히파수스의 발견에 대한 피타고라스 학파의 반응은 매우 부정적이었습니다. 히파수스는 학파의 교리를 어지럽혔기 때문에 어두운 밤에 납치를 당한 후 바다에 던져졌다는 이야기가 있습니다.
무리수의 개념이 당시 사람들에게 얼마나 큰 충격을 주었는지를 아시겠죠 ?
무리수의 수학적 중요성
하지만, 무리수의 발견은 수학의 발전에 중요한 전환점이 되었습니다.
무리수는 유리수로는 표현할 수 없는 수로, 무한 소수로 나타납니다. 예를 들어, 𝜋와 𝑒 또한 중요한 무리수입니다. 이러한 수는 대수학, 해석학, 기하학 등 여러 수학 분야에서 중요한 역할을 하고 있습니다.
